Convolution of Spectra
The spectrum function F'(ω) of a low-resolution spectrum is calculated as a convolution
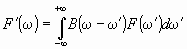 ,
,
where F(ω') is any high-resolution spectrum function described in previous paragrsph, and B(ω-ω') is the apparatus function, which simulates the effect of the aperture of the device.
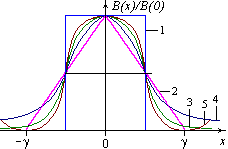
Fig. 1. Five apparatus functions B(x) used for convolution of high-resolution spectra: 1 - rectangular slit function, 2 - triangular slit function, 3 - Gaussian slit function, 4 - dispersion slit function, 5 - ideal Michelson interderometer slit function. These functions are normalized to unity; γ is a slit width or an apparatus resolution (AR).
Portal sites deals with different apparatus functions (Fig. 1):
-
Rectangular slit function
B(x) = 1/γ , if |x| ≤ γ/2 & B(x) = 0, if |x| > γ/2 ;
-
Triangular slit function
B(x) = 1/γ*(1-|x|/γ), if |x| ≤ γ & B(x) = 0, if |x| > γ ;
-
Gaussian slit functionsimilar to the Doppler line shape (see the Line profiles section)
B(x) = sqrt(ln2/π) · exp(-ln2·(x/γ)2) ; -
Dispersion slit function similar to the Lorentz line shape considered in Line profiles section
B(x) = π-1 · (γ/2) · (x2 + (γ/2)2) ,but the halfwidth γ here equals the double halfwidth D.
-
Slit function of the ideal Michelson interferometer
B(x) = sin(2πx/γ)/(πx) if x<>0 & 1 if x=0 ;
-
Difraction slit function
B(x) = sin(πx/γ)2·γ/(πx)2 if x<>0 & 1 if x=0 .
Certainly, to obtain the suitable accuracy of the low-resolution spectrum, the interval of the high-resolution spectrum should be larger than the interval of the low-resolution spectrum by, at least, a double wing of slit function. The system provides such increase of the range on low-resolution spectrum simulation by default.
